Maxwell (1981) outlined three separate domains for encoding music notation in a computer: physical, logical, and graphical. This model was later extended by the Standard Music Description Language (SMDL), an encoding system that was expressed using the Standard General Markup Language (SGML) (SGML was a precursor to XML.) SMDL built upon the Maxwell’s model and extended it to define a representation model consisting of four domains for music notation representation: logical, gestural, visual, and analytical. Although SMDL was not widely adopted, these domains remain useful for separating the functions of symbols within a music representation system.
In this model, the logical domain includes the musical content or structure including pitches, time values, articulations, dynamics, and all other elements—defined as the symbols that communicate the composer’s intentions. The gestural domain relates to a performed interpretation of the logical domain (i.e., it encodes information that may be added by a performer such as explicit realizations of “swing” or rubato). The visual domain describes the contributions of an editor, engraver, or typesetter, and encodes information about the physical appearance of the score, such as symbol locations, page layout, or font. Finally, the analytical domain covers commentary and analysis of the music document in any of the three previous domains.
MEI maintains these distinctions in its design. It is possible to, for example, encode the structural function of a note separate from its visual appearance on the page, or encode a performance realization separate from the written notation. Each of these domains may be encoded using elements and attributes inside a hierarchical text structure: the “encoding.” More importantly, a given encoding may be validated against a schema to ensure that it conforms to the rules of the encoding system. This process is explained in the next section.
XML is a hierarchical encoding system. An example of a very simple MEI XML hierarchy is shown in figure 1, using an XML representation. Elements are the core objects in an XML representation, and are represented using “tags.” These tags are a name enclosed in angle brackets (e.g., a note object is represented using the <note> tag).
Attributes of an element are used to define properties of a particular object and are represented as key-value pairs, taking the form key=”value”. A <note> object that represents “middle C” (C4) on a keyboard would be encoded in MEI as <note pname="c" oct="4"/>. (In prose, attribute and element names are distinguished by an additional “@” character on the attribute name, e.g., @pname, even though this symbol does not appear in the XML encoding.)
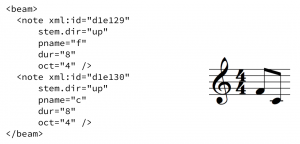
At a minimum, a valid MEI-encoded file contains two structures within the parent <mei> element: the <meiHead> and <music> elements. The <meiHead> structure contains elements that describe the work (i.e., metadata), including information about authorship, encoding standards, and provenance. The <music> structure contains information regarding the encoded music itself. The music notation is represented using XML tags, arranged in a hierarchical relationship.
MEI provides support for musical encoding by grouping the symbol definitions into modules. These modules define the elements and the rules on how these elements should interact to support a wide range of music notation encoding features. Several notation systems are supported, including common Western music notation (CWMN), mensural notation, neume notation, and guitar and lute tablature. Other modules provide support for analytical markup, editorial processes, and extended CWMN elements. A full list of the MEI modules is available in the Music Encoding Initiative Guidelines.
The structure of an MEI file can be validated to ensure that the XML used to express an encoded representation of the notation follows the rules set out by the MEI guidelines. This process, (which is common across all XML representation formats and not just MEI), uses a schema that encodes the rules and behaviors of the elements and attributes, governing where and how they may be used. There are several XML schema languages, such as DTD, W3C XML Schema, or RelaxNG. They are used in conjunction with validation software to validate whether a particular document conforms to the rules of a given schema. This can be used to determine whether an encoded document will cause problems for interoperability between different systems.
For example, an MEI file that contains lyric information as a subset of a <rest> element would not pass the validation process, since this does not conform to the rules that the MEI schema defines for the behavior of both the rest and lyric elements. This behavior is encoded in the schema to formalize the way that the music itself is known to function; in most repertoires, a lyric item attached to a rest is a musical error.
Yet in some cases, including avant-garde notation, composer-specific repertoire, or ancient notation, it may be desirable to customize the behavior of the MEI schema to include rules for validating the behavior of uncommon practices for music notation. MEI accomplishes this using a process called “schema customization,” where the behavior of the encoding can be altered to produce new schemas.
MEI is expressed in a meta-schema language developed by the Text Encoding Initiative. The “One Document Does-it-all” (ODD) format is designed to encode both the behaviors of the document encoding, and the human-readable documentation following a “literate programming” technique. From a single ODD file, a formalized schema in one of the previously-mentioned XML schema languages, as well as human-readable documentation for that schema, may be derived. The MEI schemas and guideline documentation are generated from the MEI ODD file using software developed to support the TEI project.
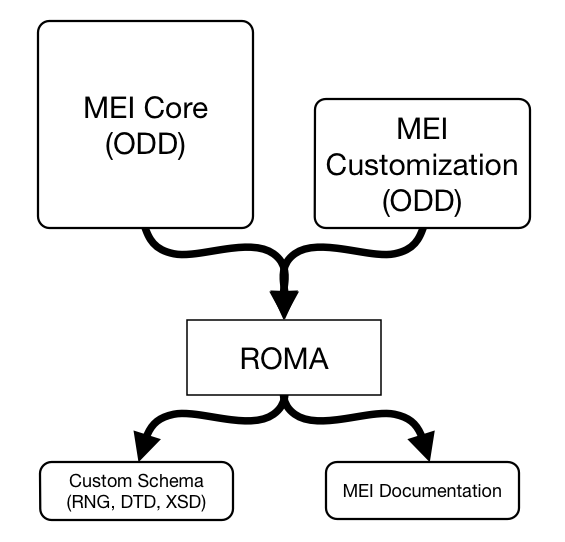
To generate a schema and documentation, two files must be provided to the Roma processor. The first is the MEI “core” ODD file. This contains the rules and definitions of the behaviors of all elements supported by MEI, in all modules. The second is a “customization” file. This file, also written using ODD, is used to modify the encoding features supported in the generated schema, either by altering the behavior of the core MEI elements or by defining new ones. A customization file may also specify that entire modules in the MEI core are not necessary to include in the resulting schema. This provides a mechanism for generating dedicated schemas for validating only CWMN notation documents, and rejecting documents that encode, for example, neume or mensural notation, or vice-versa. These customization files may be shared with other users, allowing co-operative development of customized encoding systems for different repertoires. The customization process is shown in figure 2.
This customization method is unique among music notation encoding formats. Customization and validation provide a flexible but testable means of producing MEI encodings that conform to a particular set of musical rules, and a formalized method of customizing and extending MEI make it especially suitable for encoding heterogeneous music document collections. Should new features be needed to encode a particular type of notation, it is not necessary to develop an entirely new document encoding system to support this notation. Instead, users may add or modify the behavior of the MEI core to adapt the encoding system to support new musical features.